diff --git a/docs/CS/OR-.md b/docs/CS/OR-.md
index 5eed2a27..7e70b48a 100644
--- a/docs/CS/OR-.md
+++ b/docs/CS/OR-.md
@@ -1,29 +1,188 @@
-# 规划论 | 凸优化
+# 规划论 | 非线性规划 凸优化
## 概念
+### 凸集
+
半平面的交点一定是凸集,
+- 凸规划的可行域为凸集
+
+ $$
+ h_{i}(x)=0 \quad-g_{j}(x) \leq 0 \quad \text { 凸集的交集为凸集 }
+ $$
+
+- 如果最优解存在,最优解集合也为凸集
+
+ $$
+ \begin{aligned}
+ f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}\right] \leq f\left(x_{1}^{*}\right)+(1-\lambda) f\left(x_{2}\right)=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right) & 0<\lambda<1 \\
+ f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}^{*}\right]=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right) \quad \text { 最优解的连线段均为最优解 }
+ \end{aligned}
+ $$
+
+- 推论:线性规划问题的最优解集为所有最优顶点构成的多边形。(归纳法证)
+
+ $$
+ x^{*}=\sum_{i=1}^{r} \alpha_{i} x^{*}{ }_{i} \quad \sum_{i=1}^{r} \alpha_{i}=1 \quad 0 \leq \alpha_{i} \leq 1 \quad i=1, \cdots r
+ $$
+
+ +
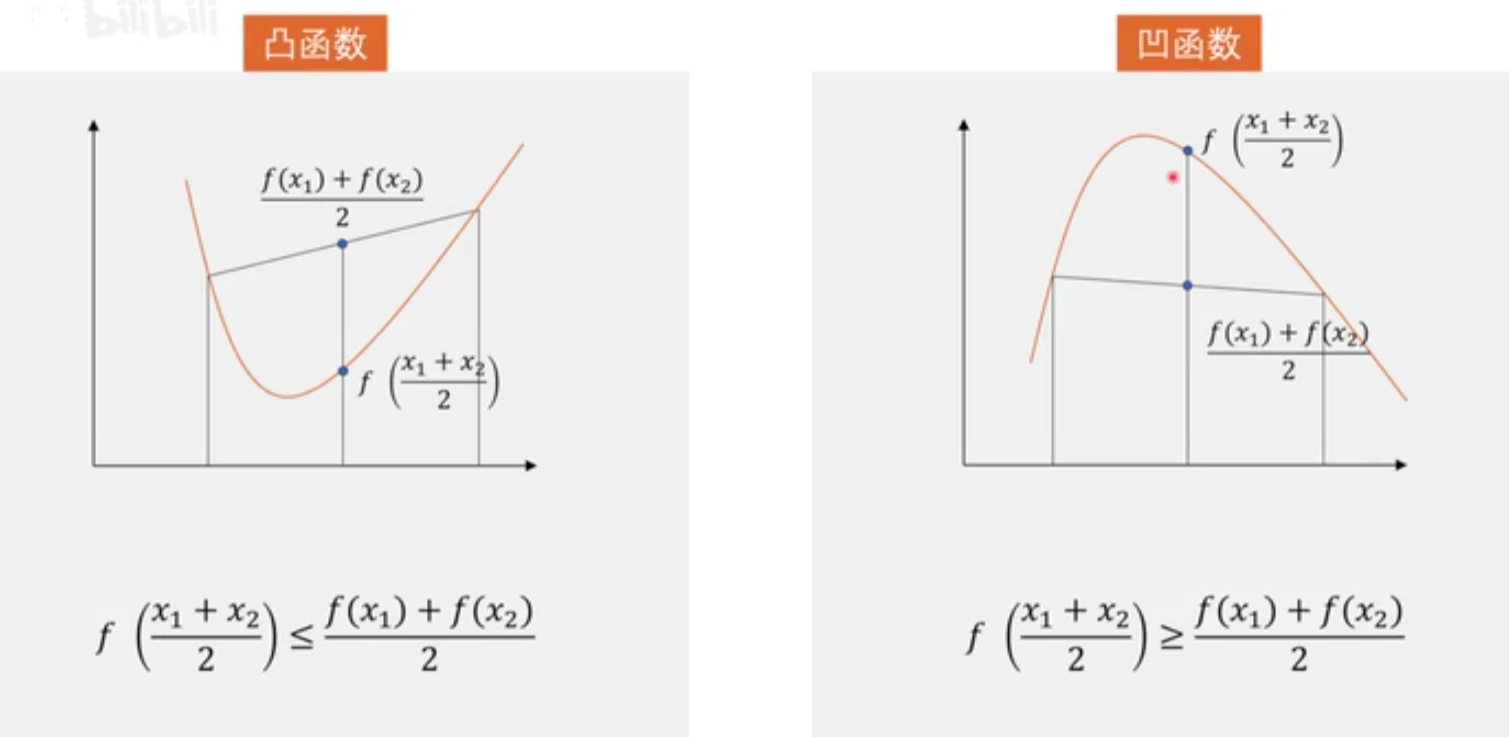
+### 凸函数
+
+设函数 $f(x)$ 在向量空间 $\mathbb{R}^n$ 的某个凸子集 $C$ 上有定义,如果对于任意 $x_1, x_2 \in C$ 和任意 $\lambda \in [0, 1]$,都有:
+
+$$
+f(\lambda x_1 + (1-\lambda) x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2)
+$$
+
+那么函数 $f(x)$ 就被称为定义在 $C$ 上的凸函数。
+
+这个定义意味着,对于定义域内的任意两点,函数曲线上的这两点之间的部分都在这两点的连线下方。换句话说,凸函数的局部最小值就是全局最小值。
+
+
+
+### 凸函数
+
+设函数 $f(x)$ 在向量空间 $\mathbb{R}^n$ 的某个凸子集 $C$ 上有定义,如果对于任意 $x_1, x_2 \in C$ 和任意 $\lambda \in [0, 1]$,都有:
+
+$$
+f(\lambda x_1 + (1-\lambda) x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2)
+$$
+
+那么函数 $f(x)$ 就被称为定义在 $C$ 上的凸函数。
+
+这个定义意味着,对于定义域内的任意两点,函数曲线上的这两点之间的部分都在这两点的连线下方。换句话说,凸函数的局部最小值就是全局最小值。
+
+ +
+#### 判定
+
+**一阶条件:**
+
+对于任意的 $x_1, x_2 \in \mathbb{R}^n$,都有
+
+$$
+f(x_2) \geq f(x_1) + \nabla f(x_1)^T (x_2 - x_1)
+$$
+
+几何意义:任何一点的切线在凸函数曲线的下方。
+
+
+
+**二阶条件:**
+
+对于任意的 $x \in \mathbb{R}^n$,都有
+
+$$
+\nabla^2 f(x) \geq 0
+$$
+
+几何意义:函数曲线向上弯曲。
+
+#### 性质
+
+- 凸函数的非负线性组合仍为凸函数。
+
+- 若 $f(x)$ 是定义在凸集 $\mathbb{R}^n$ 上的凸函数,则其 $\beta$ 水平集 $S_\beta$ 为凸集。
+> 半平面是凸集
+
+- 对于凸函数 $f(x)$,若存在 $x^* \in \mathbb{R}^n$ 满足
+
+$$
+\nabla f(x^*)^T (x - x^*) \geq 0 \quad \forall x \in \mathbb{R}^n
+$$
+
+则 $x^*$ 为 $f(x)$ 的全局最小点。
+
+> 站在山谷底看,哪里都是向上走
+
+- 对于凸目标函数,$\nabla f(x^*) = 0$ 是 $x^*$ 为极小值的充要条件。
+
+- 对于凸目标函数,局部极小点也是全局最小点。
+
+
+
+
+
+
+
+
+
+### 凸优化
+
+
+
+函数是凸函数,可行域是凸集;凹函数求最大值其实是一样的,加一个负号就可以了
+
+
+
+- 任何局部极值解也是全局最优解(目标函数为凸函数)
+
+局部极小点和全局最小点连线的目标函数值相同
+
+- 若目标函数为严格凸函数, 则如果全局最优解存在,必为唯一全局最优解。(反证法)
+ $$
+ f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}^{*}\right]<\lambda f\left(x_{1}^{*}\right)+(1-\lambda) f\left(x_{2}^{*}\right)=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right)
+ $$
+
+最优解的唯一性为数值解法提供了方便。
+
+- 凸规划下的KKT条件为最优解的充要条件
+
+
+
+
+
+
+
+* 线性规划(LP): linprog
+* 混合整数线性规划 (MILP): intlinprog
+* 二次规划(QP): quadprog
+* 二阶锥规划(SOCP): coneprog
+* 半定规划(SDP): Yalmip中调用SDP求解器
+
+* 无约束极值问题: fminunc
+* 有约束极值问题: fmincon
+
+$$
+\text { LPS } \subseteq \text { QPS } \subseteq \text { QCQPS } \subseteq \text { SOCPs } \subseteq \text { SDPs } \subseteq \text { 锥规划 } \mid \text { CPs }
+$$
+
+
+
+线性矩阵不等式LMI
+
+### 方法
+
+- 松弛到更大的区域
+- 分支定解法,拆解成多个凸集进行分布求解
+
+
-
-
-凸优化:函数是凸函数,可行域是凸集;凹函数求最大值其实是一样的,加一个负号就可以了
## 数学模型
+
+
+$$
+\min \quad f(x)
$$
-\min f(x) \\
-\text { s.t. }\left\{
-\begin{array}{c}
- \quad h_{i}(x)=0 \quad i=1,2, \ldots, m \\
-g_{j}(x) \geq 0 \quad j=1,2, \ldots, l \\
-x \in R^{n}
-\end{array}
-\right.
+$$
+\text{s.t.} \quad h_i(x) = 0 \quad i = 1, 2, ..., m
+$$
+
+$$
+\quad g_j(x) \ge 0 \quad j = 1, 2, ..., l
+$$
+
+$$
+x \in R^n
+$$
+
+将等式约束变为不等式约束,可以得到
+
+$$
+\min \quad f(x)\\
+
+\text{s.t.} \quad h_i(x) \ge 0 \quad i = 1, 2, ..., m
+\\
+\quad -h_i(x) \ge 0 \quad i = 1, 2, ..., m
+\\
+\quad g_j(x) \ge 0 \quad j = 1, 2, ..., l
+\\
+x \in R^n
$$
@@ -32,7 +191,80 @@ $$

-## 解析解法:
+
+
+
+
+**原问题**
+
+$$
+\begin{aligned}
+\min_x \ & f_0(x), x \in \mathbb{R}^n \\
+\text{s.t.} \quad & f_i(x) \le 0, \text{其中} i=1,2,3...m \\
+& h_i(x) = 0, \text{其中} i=1,2,3...q
+\end{aligned}
+$$
+
+**等价问题**
+
+$$
+\begin{aligned}
+\min_x \ \max_{\lambda, \nu} \ & L(x, \lambda, \nu)
+= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
+
+\text{s.t.} \quad & \lambda_i \ge 0 \\
+\end{aligned}
+$$
+
+
+等价性的证明
+
+$$
+x \text{在可行域内} \\
+\left\{
+\begin{array}{**lr**}
+ \lambda_i f_i(x) = 0 \quad \text{或} \lambda_i = 0 \quad\text{或} f_i(x) = 0 \\
+\nu_i h_i(x) = 0 \quad\text{或} \nu_i = 0 \quad\text{或} h_i(x) = 0
+\end{array}
+\right.
+$$
+
+* 当$x$在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)$
+* 当$x$不在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty$
+
+因此,$\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)$
+
+
+
+**对偶问题**
+
+$$
+\begin{aligned}
+&\max \limits_{\lambda,v} g(\mathbf{\lambda},\mathbf{v}) = \max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})\\
+&\text{s.t.}
+\left\{
+ \begin{array}{**lr**}
+
+ \nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
+ \lambda \geq0
+ \end{array}
+\right.
+\end{aligned}
+$$
+
+
+
+!!! note "无论原问题是什么问题,对偶问题都是凸问题"
+
+
+
+
+
+
+
+
+
+## 解析解法
### 无约束:
@@ -90,6 +322,7 @@ $$
#### **雅可比矩阵(Jacobian matrix)**
它的重要性在于它体现了一个可微方程与给出点的最优线性逼近,因此,雅可比矩阵类似于多元函数的导数
+
$$
J(\mathbf{f}) = \begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\
@@ -125,6 +358,24 @@ $$
+
+#### 判定
+
+**一阶条件:**
+
+对于任意的 $x_1, x_2 \in \mathbb{R}^n$,都有
+
+$$
+f(x_2) \geq f(x_1) + \nabla f(x_1)^T (x_2 - x_1)
+$$
+
+几何意义:任何一点的切线在凸函数曲线的下方。
+
+
+
+**二阶条件:**
+
+对于任意的 $x \in \mathbb{R}^n$,都有
+
+$$
+\nabla^2 f(x) \geq 0
+$$
+
+几何意义:函数曲线向上弯曲。
+
+#### 性质
+
+- 凸函数的非负线性组合仍为凸函数。
+
+- 若 $f(x)$ 是定义在凸集 $\mathbb{R}^n$ 上的凸函数,则其 $\beta$ 水平集 $S_\beta$ 为凸集。
+> 半平面是凸集
+
+- 对于凸函数 $f(x)$,若存在 $x^* \in \mathbb{R}^n$ 满足
+
+$$
+\nabla f(x^*)^T (x - x^*) \geq 0 \quad \forall x \in \mathbb{R}^n
+$$
+
+则 $x^*$ 为 $f(x)$ 的全局最小点。
+
+> 站在山谷底看,哪里都是向上走
+
+- 对于凸目标函数,$\nabla f(x^*) = 0$ 是 $x^*$ 为极小值的充要条件。
+
+- 对于凸目标函数,局部极小点也是全局最小点。
+
+
+
+
+
+
+
+
+
+### 凸优化
+
+
+
+函数是凸函数,可行域是凸集;凹函数求最大值其实是一样的,加一个负号就可以了
+
+
+
+- 任何局部极值解也是全局最优解(目标函数为凸函数)
+
+局部极小点和全局最小点连线的目标函数值相同
+
+- 若目标函数为严格凸函数, 则如果全局最优解存在,必为唯一全局最优解。(反证法)
+ $$
+ f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}^{*}\right]<\lambda f\left(x_{1}^{*}\right)+(1-\lambda) f\left(x_{2}^{*}\right)=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right)
+ $$
+
+最优解的唯一性为数值解法提供了方便。
+
+- 凸规划下的KKT条件为最优解的充要条件
+
+
+
+
+
+
+
+* 线性规划(LP): linprog
+* 混合整数线性规划 (MILP): intlinprog
+* 二次规划(QP): quadprog
+* 二阶锥规划(SOCP): coneprog
+* 半定规划(SDP): Yalmip中调用SDP求解器
+
+* 无约束极值问题: fminunc
+* 有约束极值问题: fmincon
+
+$$
+\text { LPS } \subseteq \text { QPS } \subseteq \text { QCQPS } \subseteq \text { SOCPs } \subseteq \text { SDPs } \subseteq \text { 锥规划 } \mid \text { CPs }
+$$
+
+
+
+线性矩阵不等式LMI
+
+### 方法
+
+- 松弛到更大的区域
+- 分支定解法,拆解成多个凸集进行分布求解
+
+
-
-
-凸优化:函数是凸函数,可行域是凸集;凹函数求最大值其实是一样的,加一个负号就可以了
## 数学模型
+
+
+$$
+\min \quad f(x)
$$
-\min f(x) \\
-\text { s.t. }\left\{
-\begin{array}{c}
- \quad h_{i}(x)=0 \quad i=1,2, \ldots, m \\
-g_{j}(x) \geq 0 \quad j=1,2, \ldots, l \\
-x \in R^{n}
-\end{array}
-\right.
+$$
+\text{s.t.} \quad h_i(x) = 0 \quad i = 1, 2, ..., m
+$$
+
+$$
+\quad g_j(x) \ge 0 \quad j = 1, 2, ..., l
+$$
+
+$$
+x \in R^n
+$$
+
+将等式约束变为不等式约束,可以得到
+
+$$
+\min \quad f(x)\\
+
+\text{s.t.} \quad h_i(x) \ge 0 \quad i = 1, 2, ..., m
+\\
+\quad -h_i(x) \ge 0 \quad i = 1, 2, ..., m
+\\
+\quad g_j(x) \ge 0 \quad j = 1, 2, ..., l
+\\
+x \in R^n
$$
@@ -32,7 +191,80 @@ $$

-## 解析解法:
+
+
+
+
+**原问题**
+
+$$
+\begin{aligned}
+\min_x \ & f_0(x), x \in \mathbb{R}^n \\
+\text{s.t.} \quad & f_i(x) \le 0, \text{其中} i=1,2,3...m \\
+& h_i(x) = 0, \text{其中} i=1,2,3...q
+\end{aligned}
+$$
+
+**等价问题**
+
+$$
+\begin{aligned}
+\min_x \ \max_{\lambda, \nu} \ & L(x, \lambda, \nu)
+= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
+
+\text{s.t.} \quad & \lambda_i \ge 0 \\
+\end{aligned}
+$$
+
+
+等价性的证明
+
+$$
+x \text{在可行域内} \\
+\left\{
+\begin{array}{**lr**}
+ \lambda_i f_i(x) = 0 \quad \text{或} \lambda_i = 0 \quad\text{或} f_i(x) = 0 \\
+\nu_i h_i(x) = 0 \quad\text{或} \nu_i = 0 \quad\text{或} h_i(x) = 0
+\end{array}
+\right.
+$$
+
+* 当$x$在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)$
+* 当$x$不在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty$
+
+因此,$\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)$
+
+
+
+**对偶问题**
+
+$$
+\begin{aligned}
+&\max \limits_{\lambda,v} g(\mathbf{\lambda},\mathbf{v}) = \max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})\\
+&\text{s.t.}
+\left\{
+ \begin{array}{**lr**}
+
+ \nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
+ \lambda \geq0
+ \end{array}
+\right.
+\end{aligned}
+$$
+
+
+
+!!! note "无论原问题是什么问题,对偶问题都是凸问题"
+
+
+
+
+
+
+
+
+
+## 解析解法
### 无约束:
@@ -90,6 +322,7 @@ $$
#### **雅可比矩阵(Jacobian matrix)**
它的重要性在于它体现了一个可微方程与给出点的最优线性逼近,因此,雅可比矩阵类似于多元函数的导数
+
$$
J(\mathbf{f}) = \begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\
@@ -125,6 +358,24 @@ $$
 +对于一个二元函数 $f(x, y)$,它的黑塞矩阵是一个 2x2 的矩阵,由函数的二阶偏导数组成。黑塞矩阵的一般形式为:
+
+$$
+H = \begin{bmatrix}
+\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
+\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
+\end{bmatrix}
+$$
+
+由于二阶偏导数具有对称性,即 $\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$,所以黑塞矩阵是一个对称矩阵。因此,我们可以将黑塞矩阵简化为:
+
+$$
+H = \begin{bmatrix}
+\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
+\frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2}
+\end{bmatrix}
+$$
+
无约束极小值问题的最优性条件
@@ -139,7 +390,6 @@ $$
### 有约束
-等式约束
$$
\begin{array}{ll}
\min & f(x) \\
@@ -148,17 +398,6 @@ $$
\end{array}
$$
-等式约束的向量形式
-$$
-\begin{array}{ll}
-\min & f(x) \\
-\text{s.t.} & h(x) = 0 \\
-& x \in \mathbb{R}^n
-\end{array}
-$$
-
-其中,$h(x) = \begin{bmatrix} h_1(x) \\ h_2(x) \\ \vdots \\ h_m(x) \end{bmatrix}$。
-
#### 拉格朗日函数
@@ -185,19 +424,12 @@ $$
+对于一个二元函数 $f(x, y)$,它的黑塞矩阵是一个 2x2 的矩阵,由函数的二阶偏导数组成。黑塞矩阵的一般形式为:
+
+$$
+H = \begin{bmatrix}
+\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
+\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
+\end{bmatrix}
+$$
+
+由于二阶偏导数具有对称性,即 $\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$,所以黑塞矩阵是一个对称矩阵。因此,我们可以将黑塞矩阵简化为:
+
+$$
+H = \begin{bmatrix}
+\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
+\frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2}
+\end{bmatrix}
+$$
+
无约束极小值问题的最优性条件
@@ -139,7 +390,6 @@ $$
### 有约束
-等式约束
$$
\begin{array}{ll}
\min & f(x) \\
@@ -148,17 +398,6 @@ $$
\end{array}
$$
-等式约束的向量形式
-$$
-\begin{array}{ll}
-\min & f(x) \\
-\text{s.t.} & h(x) = 0 \\
-& x \in \mathbb{R}^n
-\end{array}
-$$
-
-其中,$h(x) = \begin{bmatrix} h_1(x) \\ h_2(x) \\ \vdots \\ h_m(x) \end{bmatrix}$。
-
#### 拉格朗日函数
@@ -185,19 +424,12 @@ $$
 -只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为0
-
-
-
-
-
-
-
-
+> 只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为0
不等式约束
+
$$
\begin{array}{ll}
\min & f(x) \\
@@ -208,9 +440,7 @@ $$
-目标函数减小的充分条件
-约束$g(x) = 0$强约束
@@ -293,96 +523,392 @@ $B^T$是$R^n$中一组基,由$m$个$n$维列向量组成,只存在两种情
-#### **Fritz John定理**
+#### **Fritz John定理**——局部极小点必要条件
+
+$$
+\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \mu_i^* \nabla h_i(x^*) + \sum_{i=1}^m \mu_i^{**} \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+$$
+\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m (\mu_i^* - \mu_i^{**}) \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+$$
+\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+其中,$\gamma_i = \mu_i^* - \mu_i^{**}$,并且有:
+
+$$
+\mu_i^* \ge 0 \quad \mu_i^{**} \ge 0 \quad \Longrightarrow \gamma_i = \mu_i^* - \mu_i^{**} \text{ 无符号约束 } \quad i = 1, 2, ..., p
+$$
+
+注意,$\mu_0$、$\mu_j$、$\gamma_i$ 不可同时为 0。
+
+> $\gamma_i$无符号约束,所以前边是加号或是减号都不影响
+
+
+
+
+
+假设 $x^*$ 是局部极小点,存在不全为零的 $\mu_j^* (j=0, 1, 2, ..., m)$ 和 $\gamma_i (i=0, 1, 2, ..., p)$,满足:
+
+$$
+\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0 \quad 拉格朗日条件
+$$
-设$X^*$是非线性规划的局部最优点,函数$f(x)$和$g_j(x)(j=1,2,...,l)$在点$X^*$有连续一阶偏导,则必然存在不全为零的数$\mu_0, \mu_1, \mu_2, ..., \mu_l$,使
+$$
+\mu_j^* g_j(x^*) = 0 \quad j = 1, 2, ..., m \quad 互补松弛条件\\
+\gamma_i h_i(x^*) = 0 \quad i = 1, 2, ..., p \quad 等式互补松弛
+$$
$$
-\begin{align}
-\mu_0 \nabla f(X^*) - \sum_{j=1}^l \mu_j \nabla g_j(X^*) = 0 \quad &Lagrange函数驻点条件\\
-\mu_j g_j(X^*) = 0 \quad (j=1,2,...,l) \quad &互补松弛条件\\
-\mu_0 \ge 0, \mu_j \ge 0 \quad (j=1,2,...,l) \quad &强非负条件
-\end{align}
+\mu_j^* \ge 0 \quad j = 0, 1, ..., m\\
+\sum_{j=0}^l \mu_j^* + \sum_{i=1}^m |\gamma_i^* |\neq 0 \quad 强非负条件
$$
+
+
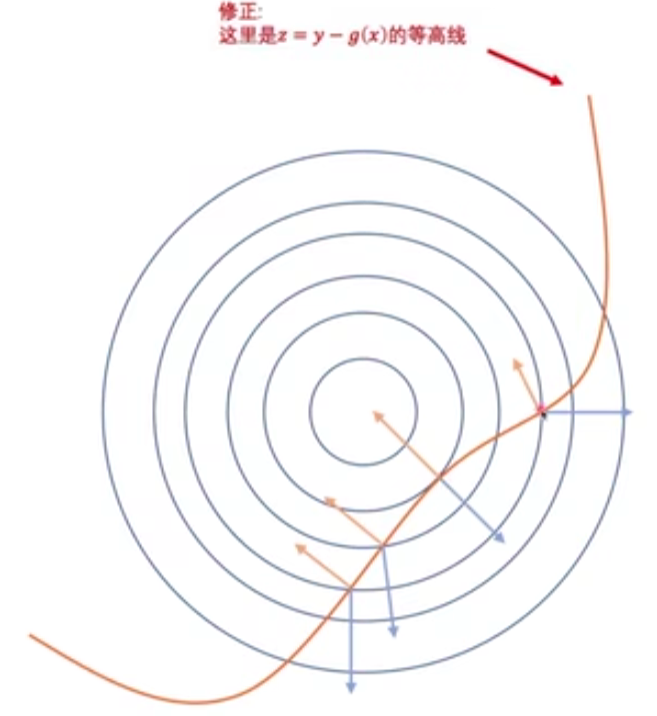
-只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为0
-
-
-
-
-
-
-
-
+> 只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为0
不等式约束
+
$$
\begin{array}{ll}
\min & f(x) \\
@@ -208,9 +440,7 @@ $$
-目标函数减小的充分条件
-约束$g(x) = 0$强约束
@@ -293,96 +523,392 @@ $B^T$是$R^n$中一组基,由$m$个$n$维列向量组成,只存在两种情
-#### **Fritz John定理**
+#### **Fritz John定理**——局部极小点必要条件
+
+$$
+\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \mu_i^* \nabla h_i(x^*) + \sum_{i=1}^m \mu_i^{**} \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+$$
+\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m (\mu_i^* - \mu_i^{**}) \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+$$
+\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+其中,$\gamma_i = \mu_i^* - \mu_i^{**}$,并且有:
+
+$$
+\mu_i^* \ge 0 \quad \mu_i^{**} \ge 0 \quad \Longrightarrow \gamma_i = \mu_i^* - \mu_i^{**} \text{ 无符号约束 } \quad i = 1, 2, ..., p
+$$
+
+注意,$\mu_0$、$\mu_j$、$\gamma_i$ 不可同时为 0。
+
+> $\gamma_i$无符号约束,所以前边是加号或是减号都不影响
+
+
+
+
+
+假设 $x^*$ 是局部极小点,存在不全为零的 $\mu_j^* (j=0, 1, 2, ..., m)$ 和 $\gamma_i (i=0, 1, 2, ..., p)$,满足:
+
+$$
+\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0 \quad 拉格朗日条件
+$$
-设$X^*$是非线性规划的局部最优点,函数$f(x)$和$g_j(x)(j=1,2,...,l)$在点$X^*$有连续一阶偏导,则必然存在不全为零的数$\mu_0, \mu_1, \mu_2, ..., \mu_l$,使
+$$
+\mu_j^* g_j(x^*) = 0 \quad j = 1, 2, ..., m \quad 互补松弛条件\\
+\gamma_i h_i(x^*) = 0 \quad i = 1, 2, ..., p \quad 等式互补松弛
+$$
$$
-\begin{align}
-\mu_0 \nabla f(X^*) - \sum_{j=1}^l \mu_j \nabla g_j(X^*) = 0 \quad &Lagrange函数驻点条件\\
-\mu_j g_j(X^*) = 0 \quad (j=1,2,...,l) \quad &互补松弛条件\\
-\mu_0 \ge 0, \mu_j \ge 0 \quad (j=1,2,...,l) \quad &强非负条件
-\end{align}
+\mu_j^* \ge 0 \quad j = 0, 1, ..., m\\
+\sum_{j=0}^l \mu_j^* + \sum_{i=1}^m |\gamma_i^* |\neq 0 \quad 强非负条件
$$
+
+
 -> 红线上的梯度,在$\lambda_i > 0$的情况下是不可能和目标函数相抵消的,所以只能是$\lambda_i =0$(松弛的约束条件),然后让$x^*$处的约束条件(紧致的约束条件)线性组合为负梯度
+> - 对于紧致的约束条件,$g(x^*) = 0$,但是$\sum_{j=1}^l \mu_j \nabla g_j(X^*)$应该等于负梯度,$\lambda_i \neq 0$
+>
+> - 对于松弛的约束条件,将$x^*$带入方程,一定是小于(大于)0的,最重要的是要让梯度在$\lambda_i$的作用下不对结果起作用;
-> 红线上的梯度,在$\lambda_i > 0$的情况下是不可能和目标函数相抵消的,所以只能是$\lambda_i =0$(松弛的约束条件),然后让$x^*$处的约束条件(紧致的约束条件)线性组合为负梯度
+> - 对于紧致的约束条件,$g(x^*) = 0$,但是$\sum_{j=1}^l \mu_j \nabla g_j(X^*)$应该等于负梯度,$\lambda_i \neq 0$
+>
+> - 对于松弛的约束条件,将$x^*$带入方程,一定是小于(大于)0的,最重要的是要让梯度在$\lambda_i$的作用下不对结果起作用;
在红线上的,在$\lambda_i>0$的情况下,是不能实现与负梯度相同的,所以$\lambda_i=0$
-* Fritz John条件是由Gordan引理矩阵展开得到。Gordan引理只对起作用约束做了说明,Fritz John定理采用互补松弛条件将起作用约束引入,取对应参数为0改良得到。
-* 判断一个点是不是Fritz John点的步骤就是找到对应的函数梯度,带入公式看是否能找到不全为零的数使得方程成立。
-* 如果$\mu_j=0$,$pf_j(x)$就从Fritz John条件中消去,说明在所讨论的点$X^*$处,起作用约束的梯度线性相关,即该点Fritz John条件失效,因此需要对讨论点处起作用约束的梯度附加上线性无关的约束条件,保证$\mu_j>0$,这样就引出了库恩-塔克条件。
-**原问题**
+
+#### Slater条件——强对偶的充分条件
+
+Slater条件是指:存在一个点$x \in relint D$,$relint D$表示可行域$D$的相对内部。
+
+使得$f_i(x) < 0$,其中$i = 1, 2, 3, ..., m$,$Ax = b$。
+
+换句话说,Slater条件是指在可行域的内部存在一个点,使得所有约束函数的值都小于零。这个条件在线性规划和非线性规划中都有应用,是判断**对偶问题是否具有强对偶性的充分条件之一**。
+
+> 内部存在点
+
+ +
+
+
+#### KKT条件——强对偶的必要条件
+
+正则条件(regular condition)是指起作用约束$\nabla g_{i^*}(x^*)$线性无关。
+
+性质:若极小值$x^*$满足正则条件,则KKT条件成立。证明:$x^*$满足正则条件,Fritz John条件中的$\mu_i>0$。
+
+Kuhn-Tucker定理:若$x^*$是局部极小点,且满足正则条件(约束规格),则Kuhn-Tucker条件成立。
+
+
+
+
+
+
+
+##### **KKT条件的矩阵形式**
+
+$$
+y^* =
+
+\begin{bmatrix}
+y_1^* \\
+y_2^* \\
+\vdots \\
+y_m^*
+\end{bmatrix}
+
+\quad
+h(x)=
+\begin{bmatrix}
+h_1(x) \\
+h_2(x) \\
+\vdots \\
+h_m(x)
+\end{bmatrix}
+
+\quad
+\mu^* =
+\begin{bmatrix}
+\mu_1^* \\
+\mu_2^* \\
+\vdots \\
+\mu_n^*
+\end{bmatrix}
+
+\quad
+g(x) =
+\begin{bmatrix}
+g_1(x) \\
+g_2(x) \\
+\vdots \\
+g_n(x)
+\end{bmatrix}
+$$
+
+$$
+\nabla h(x) =
+\begin{bmatrix}
+\nabla h_1(x) & \nabla h_2(x) & \cdots & \nabla h_m(x)
+\end{bmatrix}
+$$
+
+$$
+\nabla g(x) =
+\begin{bmatrix}
+\nabla g_1(x) & \nabla g_2(x) & \cdots & \nabla g_l(x)
+\end{bmatrix}
+=
+\begin{bmatrix}
+\frac{\partial g_1}{\partial x_1} & \frac{\partial g_2}{\partial x_1} & \cdots & \frac{\partial g_l}{\partial x_1} \\
+\frac{\partial g_1}{\partial x_2} & \frac{\partial g_2}{\partial x_2} & \cdots & \frac{\partial g_l}{\partial x_2} \\
+\vdots & \vdots & \ddots & \vdots \\
+\frac{\partial g_1}{\partial x_n} & \frac{\partial g_2}{\partial x_n} & \cdots & \frac{\partial g_l}{\partial x_n}
+\end{bmatrix}^T
+$$
+
+**Lagrange驻点条件**
+
+$$
+\nabla f(x^*) - \nabla h(x^*)y^* - \nabla g(x^*)\mu^* = 0
+$$
+
+**互补松弛条件**
+
+$$
+\mu^* \odot g(x^*) = 0 \\\Leftrightarrow \mu_j^* g_j(x^*) = 0 \quad j=1,2,...,l
+$$
+
+**非负条件**
+
+$$
+\mu^* \geq 0
+$$
+
+**可行性条件**
+
$$
\begin{aligned}
-\min_x \ & f_0(x), x \in \mathbb{R}^n \\
-\text{s.t.} \quad & f_i(x) \le 0, \text{其中} i=1,2,3...m \\
-& h_i(x) = 0, \text{其中} i=1,2,3...q
+h(x^*) &= 0 \\
+g(x^*) &\geq 0
\end{aligned}
$$
-**等价问题**
+
+
+
+
+#### 例题
+
+$$
+\begin{array}{ll}
+\min & f(x_1, x_2) = (x_1 - 2)^2 + x_2^2 \\
+\text{s.t.} & x_2 \le x_1 + 2 \\
+& x_2 \ge x_1^2 + 1 \\
+& x_1 \ge 0 \quad x_2 \ge 0
+\end{array}
$$
-\begin{aligned}
-\min_x \ \max_{\lambda, \nu} \ & L(x, \lambda, \nu)
-= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
-\text{s.t.} \quad & \lambda_i \ge 0 \\
-\end{aligned}
+**列出向量**
+$$
+f(\mathbf{x}) = (x_1 - 2)^2 + x_2^2
$$
+$$
+\nabla f(\mathbf{x}) = \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right]
+$$
-等价性的证明
$$
-x \text{在可行域内} \\
-\left\{
-\begin{array}{**lr**}
- \lambda_i f_i(x) = 0 \quad \text{或} \lambda_i = 0 \quad\text{或} f_i(x) = 0 \\
-\nu_i h_i(x) = 0 \quad\text{或} \nu_i = 0 \quad\text{或} h_i(x) = 0
+\mathbf{g}(\mathbf{x}) = \left[ \begin{array}{c} x_1 - x_2 + 2 \\ -x_1^2 + x_2 - 1 \\ x_1 \\ x_2 \end{array} \right]
+$$
+
+$$
+\nabla \mathbf{g}(\mathbf{x}) = \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right]
+$$
+
+**列出题目条件**
+$$
+\nabla f(x^*) - \nabla h(x^*) y^* - \nabla g(x^*) \mu^* = 0
+$$
+
+$$
+\Longrightarrow \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right] - \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \mu_1 \\ \mu_2 \\ \mu_3 \\ \mu_4 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
+$$
+
+$$
+\mu^* \otimes g(x^*) = 0 \quad \Longrightarrow \left[ \begin{array}{c} \mu_1 (x_1 - x_2 + 2) \\ \mu_2 (-x_1^2 + x_2 - 1) \\ \mu_3 x_1 \\ \mu_4 x_2 \end{array} \right] = 0
+$$
+
+$$
+g(x^*) \ge 0 \quad \mu^* \ge 0
+$$
+
+**得出方程**
+$$
+\begin{array}{ll}
+2(x_1 - 2) - \mu_1 + 2 \mu_2 x_1 - \mu_3 &= 0 \\
+2x_2 + \mu_1 - \mu_2 - \mu_4 &= 0 \\
+\mu_1 (x_1 - x_2 + 2) &= 0 \\
+\mu_2 (-x_1^2 + x_2 - 1) &= 0 \\
+\mu_3 x_1 &= 0 \\
+\mu_4 x_2 &= 0 \\
+\mu_j &\ge 0 \quad j = 1, 2, 3, 4 \\
+x_2 &\le x_1 + 2 \\
+x_2 &\ge x_1^2 + 1 \\
+x_1, x_2 &\ge 0
\end{array}
-\right.
$$
-* 当$x$在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)$
-* 当$x$不在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty$
+**求解方程**
+观察可得:$\mu_1 = \mu_3 = \mu_4 = 0$(松弛性)
-因此,$\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)$
+所以有:
+$$
+(1 + \mu_2) x_1 - 2 = 0
+$$
+$$
+2x_2 - \mu_2 = 0
+$$
+
+$$
+-x_1^2 + x_2 - 1 = 0
+$$
+
+求解得:
+
+$$
+\mu_2^* = 2.6219 \quad x_1^* = 0.5536 \quad x_2^* = 1.3064
+$$
+
+$$
+f(x^*) = 3.7989
+$$
+
+### 在机器学习中的应用
+
+最大熵
+
+交叉熵
+
+
+
+## 数值解法
+
+包括基于梯度的数值解法,如最速下降法、牛顿法、拟牛顿法等,以及有约束极值问题的数值解法,如可行方向法、制约函数法等。
+
+
+
+
+
+#### KKT条件——强对偶的必要条件
+
+正则条件(regular condition)是指起作用约束$\nabla g_{i^*}(x^*)$线性无关。
+
+性质:若极小值$x^*$满足正则条件,则KKT条件成立。证明:$x^*$满足正则条件,Fritz John条件中的$\mu_i>0$。
+
+Kuhn-Tucker定理:若$x^*$是局部极小点,且满足正则条件(约束规格),则Kuhn-Tucker条件成立。
+
+
+
+
+
+
+
+##### **KKT条件的矩阵形式**
+
+$$
+y^* =
+
+\begin{bmatrix}
+y_1^* \\
+y_2^* \\
+\vdots \\
+y_m^*
+\end{bmatrix}
+
+\quad
+h(x)=
+\begin{bmatrix}
+h_1(x) \\
+h_2(x) \\
+\vdots \\
+h_m(x)
+\end{bmatrix}
+
+\quad
+\mu^* =
+\begin{bmatrix}
+\mu_1^* \\
+\mu_2^* \\
+\vdots \\
+\mu_n^*
+\end{bmatrix}
+
+\quad
+g(x) =
+\begin{bmatrix}
+g_1(x) \\
+g_2(x) \\
+\vdots \\
+g_n(x)
+\end{bmatrix}
+$$
+
+$$
+\nabla h(x) =
+\begin{bmatrix}
+\nabla h_1(x) & \nabla h_2(x) & \cdots & \nabla h_m(x)
+\end{bmatrix}
+$$
+
+$$
+\nabla g(x) =
+\begin{bmatrix}
+\nabla g_1(x) & \nabla g_2(x) & \cdots & \nabla g_l(x)
+\end{bmatrix}
+=
+\begin{bmatrix}
+\frac{\partial g_1}{\partial x_1} & \frac{\partial g_2}{\partial x_1} & \cdots & \frac{\partial g_l}{\partial x_1} \\
+\frac{\partial g_1}{\partial x_2} & \frac{\partial g_2}{\partial x_2} & \cdots & \frac{\partial g_l}{\partial x_2} \\
+\vdots & \vdots & \ddots & \vdots \\
+\frac{\partial g_1}{\partial x_n} & \frac{\partial g_2}{\partial x_n} & \cdots & \frac{\partial g_l}{\partial x_n}
+\end{bmatrix}^T
+$$
+
+**Lagrange驻点条件**
+
+$$
+\nabla f(x^*) - \nabla h(x^*)y^* - \nabla g(x^*)\mu^* = 0
+$$
+
+**互补松弛条件**
+
+$$
+\mu^* \odot g(x^*) = 0 \\\Leftrightarrow \mu_j^* g_j(x^*) = 0 \quad j=1,2,...,l
+$$
+
+**非负条件**
+
+$$
+\mu^* \geq 0
+$$
+
+**可行性条件**
+
$$
\begin{aligned}
-\min_x \ & f_0(x), x \in \mathbb{R}^n \\
-\text{s.t.} \quad & f_i(x) \le 0, \text{其中} i=1,2,3...m \\
-& h_i(x) = 0, \text{其中} i=1,2,3...q
+h(x^*) &= 0 \\
+g(x^*) &\geq 0
\end{aligned}
$$
-**等价问题**
+
+
+
+
+#### 例题
+
+$$
+\begin{array}{ll}
+\min & f(x_1, x_2) = (x_1 - 2)^2 + x_2^2 \\
+\text{s.t.} & x_2 \le x_1 + 2 \\
+& x_2 \ge x_1^2 + 1 \\
+& x_1 \ge 0 \quad x_2 \ge 0
+\end{array}
$$
-\begin{aligned}
-\min_x \ \max_{\lambda, \nu} \ & L(x, \lambda, \nu)
-= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
-\text{s.t.} \quad & \lambda_i \ge 0 \\
-\end{aligned}
+**列出向量**
+$$
+f(\mathbf{x}) = (x_1 - 2)^2 + x_2^2
$$
+$$
+\nabla f(\mathbf{x}) = \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right]
+$$
-等价性的证明
$$
-x \text{在可行域内} \\
-\left\{
-\begin{array}{**lr**}
- \lambda_i f_i(x) = 0 \quad \text{或} \lambda_i = 0 \quad\text{或} f_i(x) = 0 \\
-\nu_i h_i(x) = 0 \quad\text{或} \nu_i = 0 \quad\text{或} h_i(x) = 0
+\mathbf{g}(\mathbf{x}) = \left[ \begin{array}{c} x_1 - x_2 + 2 \\ -x_1^2 + x_2 - 1 \\ x_1 \\ x_2 \end{array} \right]
+$$
+
+$$
+\nabla \mathbf{g}(\mathbf{x}) = \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right]
+$$
+
+**列出题目条件**
+$$
+\nabla f(x^*) - \nabla h(x^*) y^* - \nabla g(x^*) \mu^* = 0
+$$
+
+$$
+\Longrightarrow \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right] - \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \mu_1 \\ \mu_2 \\ \mu_3 \\ \mu_4 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
+$$
+
+$$
+\mu^* \otimes g(x^*) = 0 \quad \Longrightarrow \left[ \begin{array}{c} \mu_1 (x_1 - x_2 + 2) \\ \mu_2 (-x_1^2 + x_2 - 1) \\ \mu_3 x_1 \\ \mu_4 x_2 \end{array} \right] = 0
+$$
+
+$$
+g(x^*) \ge 0 \quad \mu^* \ge 0
+$$
+
+**得出方程**
+$$
+\begin{array}{ll}
+2(x_1 - 2) - \mu_1 + 2 \mu_2 x_1 - \mu_3 &= 0 \\
+2x_2 + \mu_1 - \mu_2 - \mu_4 &= 0 \\
+\mu_1 (x_1 - x_2 + 2) &= 0 \\
+\mu_2 (-x_1^2 + x_2 - 1) &= 0 \\
+\mu_3 x_1 &= 0 \\
+\mu_4 x_2 &= 0 \\
+\mu_j &\ge 0 \quad j = 1, 2, 3, 4 \\
+x_2 &\le x_1 + 2 \\
+x_2 &\ge x_1^2 + 1 \\
+x_1, x_2 &\ge 0
\end{array}
-\right.
$$
-* 当$x$在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)$
-* 当$x$不在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty$
+**求解方程**
+观察可得:$\mu_1 = \mu_3 = \mu_4 = 0$(松弛性)
-因此,$\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)$
+所以有:
+$$
+(1 + \mu_2) x_1 - 2 = 0
+$$
+$$
+2x_2 - \mu_2 = 0
+$$
+
+$$
+-x_1^2 + x_2 - 1 = 0
+$$
+
+求解得:
+
+$$
+\mu_2^* = 2.6219 \quad x_1^* = 0.5536 \quad x_2^* = 1.3064
+$$
+
+$$
+f(x^*) = 3.7989
+$$
+
+### 在机器学习中的应用
+
+最大熵
+
+交叉熵
+
+
+
+## 数值解法
+
+包括基于梯度的数值解法,如最速下降法、牛顿法、拟牛顿法等,以及有约束极值问题的数值解法,如可行方向法、制约函数法等。
+
+ +
+### 基于梯度方法
+
+#### 最速下降法——迭代初期
+
+
+
+极小值附近的等值面是椭球面
+
+$X^T \cdot \mathbf{H} \cdot X = c$
+
+- 如果$\mathbf{H}$是对角矩阵,则显然是椭圆
+- 如果不是的话,相似对角化以后$X^TM^T \ \Lambda\mathbf{}\ M X = c$
+
+
+
+
+
+
+
+
+
+#### 牛顿法——极值点附近
+
+* 设计思想:近似为二次问题。
-**对偶问题**
$$
\begin{aligned}
-&\max \limits_{\lambda,v} g(\mathbf{\lambda},\mathbf{v}) = \max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})\\
-&\text{s.t.}
-\left\{
- \begin{array}{**lr**}
-
- \nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
- \lambda \geq0
- \end{array}
-\right.
+&f(x) \approx f\left(x^{(k)}\right)+\nabla f\left(x^{(k)}\right)^{T}\left(x-x^{(k)}\right)+\frac{1}{2}\left(x-x^{(k)}\right)^{T} \nabla^{2} f\left(x^{(k)}\right)\left(x-x^{(k)}\right) \\
+&\text { 驻点条件 } \Longrightarrow \nabla f(x) \approx \nabla f\left(x^{(k)}\right)+\nabla^{2} f\left(x^{(k)}\right)\left(x-x^{(k)}\right) \approx 0 \\
+&\text { 迭代公式 } \Longrightarrow x^{(k+1)} \approx x^{(k)}-\left[\nabla^{2} f\left(x^{(k)}\right)\right]^{-1} \nabla f\left(x^{(k)}\right) \\
+&\text { 迭代方向 } \Longrightarrow p^{(k)}=-\left[\nabla^{2} f\left(x^{(k)}\right)\right]^{-1} \nabla f\left(x^{(k)}\right) \quad \text { 牛顿方向 }
\end{aligned}
$$
-
-!!! note "无论原问题是什么问题,对偶问题都是凸问题"
+优点:极值点附近收敛速率快。
+缺点:计算量大,需要求二阶导数和Hessian矩阵逆。
+远离极值点时,不一定是下降方向,需采用进一步修正。
+应用场合:二次目标函数或极值点附近。
+* 设$A$为对称矩阵,二次函数 $f(x)=\frac{1}{2} x^T A x+b^T x+c$
+* 驻点方程: $\nabla f(x)=Ax+b=0$
+ + 有解: $\text{rank} A=\text{rank}[A \quad b]$
+ + 无解: $\text{rank} A \neq \text{rank}[A \quad b]$
+* Hessian矩阵: $\nabla^2 f(x)=A$
-## 数值解法
+例: 抛物面
+
+* (1) $A>0$ 椭球面: $x^*=A^{-1} b$ 唯一极小点
+* (2) $A \geq 0 \quad \& \quad \text{rank} A\left|\lambda_{\text {min }}\right| \quad \lambda_{\text {min }} \text { 为 } \nabla^2 f\left(x^{(k)}\right) \text { 最小负特征值 }$
+* $\mu \rightarrow 0$ : 牛顿法
+* $\mu \rightarrow \infty$ : 最速下降法
+* 如果不求特征值,可以从较小的 $\mu$ 值试探
+
+
+
+#### 拟牛顿法
+
+
+
+**目标: 数值法求解Hessian矩阵的逆**
+
+* 由Davidon提出, Fletcher和Powell改进, 也称DFP算法。
+* 迭代方向: $p^{(k)}=-H_{k} \nabla f\left(x^{(k)}\right)$
+* $H_{k+1}=H_{k}+\Delta H_{k} \quad H_{0}=I$
+* $\Delta H_{k}=\frac{8 s_{k}^{T} s_{k}}{s_{k}^{T} H_{k} \gamma_{k}^{T} H_{k}} H_{k} \gamma_{k} \gamma_{k}^{T} H_{k} \quad s_{k}=x^{(k+1)}-x^{(k)}$
+* $\gamma_{k}=\nabla f\left(x^{(k+1)}\right)-\nabla f\left(x^{(k)}\right)$
+
+可以证明:
+
+- 1、$H_{k}$ 满足拟牛顿条件, 为Hessian矩阵的逆。
+
+* 2、当目标函数为严格凸二次函数时, 可经有限步迭代收敛于极值(二次终止性)。为什么不是1步?
+
+
+
+
+
+#### 共轭梯度法
+
+前面的方法需要求Hessian矩阵的逆
+
+
+
+
+
+
+
+
+
+### 启发式方法
-包括基于梯度的数值解法,如最速下降法、牛顿法、拟牛顿法等,以及有约束极值问题的数值解法,如可行方向法、制约函数法等。
\ No newline at end of file
+
+### 基于梯度方法
+
+#### 最速下降法——迭代初期
+
+
+
+极小值附近的等值面是椭球面
+
+$X^T \cdot \mathbf{H} \cdot X = c$
+
+- 如果$\mathbf{H}$是对角矩阵,则显然是椭圆
+- 如果不是的话,相似对角化以后$X^TM^T \ \Lambda\mathbf{}\ M X = c$
+
+
+
+
+
+
+
+
+
+#### 牛顿法——极值点附近
+
+* 设计思想:近似为二次问题。
-**对偶问题**
$$
\begin{aligned}
-&\max \limits_{\lambda,v} g(\mathbf{\lambda},\mathbf{v}) = \max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})\\
-&\text{s.t.}
-\left\{
- \begin{array}{**lr**}
-
- \nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
- \lambda \geq0
- \end{array}
-\right.
+&f(x) \approx f\left(x^{(k)}\right)+\nabla f\left(x^{(k)}\right)^{T}\left(x-x^{(k)}\right)+\frac{1}{2}\left(x-x^{(k)}\right)^{T} \nabla^{2} f\left(x^{(k)}\right)\left(x-x^{(k)}\right) \\
+&\text { 驻点条件 } \Longrightarrow \nabla f(x) \approx \nabla f\left(x^{(k)}\right)+\nabla^{2} f\left(x^{(k)}\right)\left(x-x^{(k)}\right) \approx 0 \\
+&\text { 迭代公式 } \Longrightarrow x^{(k+1)} \approx x^{(k)}-\left[\nabla^{2} f\left(x^{(k)}\right)\right]^{-1} \nabla f\left(x^{(k)}\right) \\
+&\text { 迭代方向 } \Longrightarrow p^{(k)}=-\left[\nabla^{2} f\left(x^{(k)}\right)\right]^{-1} \nabla f\left(x^{(k)}\right) \quad \text { 牛顿方向 }
\end{aligned}
$$
-
-!!! note "无论原问题是什么问题,对偶问题都是凸问题"
+优点:极值点附近收敛速率快。
+缺点:计算量大,需要求二阶导数和Hessian矩阵逆。
+远离极值点时,不一定是下降方向,需采用进一步修正。
+应用场合:二次目标函数或极值点附近。
+* 设$A$为对称矩阵,二次函数 $f(x)=\frac{1}{2} x^T A x+b^T x+c$
+* 驻点方程: $\nabla f(x)=Ax+b=0$
+ + 有解: $\text{rank} A=\text{rank}[A \quad b]$
+ + 无解: $\text{rank} A \neq \text{rank}[A \quad b]$
+* Hessian矩阵: $\nabla^2 f(x)=A$
-## 数值解法
+例: 抛物面
+
+* (1) $A>0$ 椭球面: $x^*=A^{-1} b$ 唯一极小点
+* (2) $A \geq 0 \quad \& \quad \text{rank} A\left|\lambda_{\text {min }}\right| \quad \lambda_{\text {min }} \text { 为 } \nabla^2 f\left(x^{(k)}\right) \text { 最小负特征值 }$
+* $\mu \rightarrow 0$ : 牛顿法
+* $\mu \rightarrow \infty$ : 最速下降法
+* 如果不求特征值,可以从较小的 $\mu$ 值试探
+
+
+
+#### 拟牛顿法
+
+
+
+**目标: 数值法求解Hessian矩阵的逆**
+
+* 由Davidon提出, Fletcher和Powell改进, 也称DFP算法。
+* 迭代方向: $p^{(k)}=-H_{k} \nabla f\left(x^{(k)}\right)$
+* $H_{k+1}=H_{k}+\Delta H_{k} \quad H_{0}=I$
+* $\Delta H_{k}=\frac{8 s_{k}^{T} s_{k}}{s_{k}^{T} H_{k} \gamma_{k}^{T} H_{k}} H_{k} \gamma_{k} \gamma_{k}^{T} H_{k} \quad s_{k}=x^{(k+1)}-x^{(k)}$
+* $\gamma_{k}=\nabla f\left(x^{(k+1)}\right)-\nabla f\left(x^{(k)}\right)$
+
+可以证明:
+
+- 1、$H_{k}$ 满足拟牛顿条件, 为Hessian矩阵的逆。
+
+* 2、当目标函数为严格凸二次函数时, 可经有限步迭代收敛于极值(二次终止性)。为什么不是1步?
+
+
+
+
+
+#### 共轭梯度法
+
+前面的方法需要求Hessian矩阵的逆
+
+
+
+
+
+
+
+
+
+### 启发式方法
-包括基于梯度的数值解法,如最速下降法、牛顿法、拟牛顿法等,以及有约束极值问题的数值解法,如可行方向法、制约函数法等。
\ No newline at end of file
 +
+### 凸函数
+
+设函数 $f(x)$ 在向量空间 $\mathbb{R}^n$ 的某个凸子集 $C$ 上有定义,如果对于任意 $x_1, x_2 \in C$ 和任意 $\lambda \in [0, 1]$,都有:
+
+$$
+f(\lambda x_1 + (1-\lambda) x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2)
+$$
+
+那么函数 $f(x)$ 就被称为定义在 $C$ 上的凸函数。
+
+这个定义意味着,对于定义域内的任意两点,函数曲线上的这两点之间的部分都在这两点的连线下方。换句话说,凸函数的局部最小值就是全局最小值。
+
+
+
+### 凸函数
+
+设函数 $f(x)$ 在向量空间 $\mathbb{R}^n$ 的某个凸子集 $C$ 上有定义,如果对于任意 $x_1, x_2 \in C$ 和任意 $\lambda \in [0, 1]$,都有:
+
+$$
+f(\lambda x_1 + (1-\lambda) x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2)
+$$
+
+那么函数 $f(x)$ 就被称为定义在 $C$ 上的凸函数。
+
+这个定义意味着,对于定义域内的任意两点,函数曲线上的这两点之间的部分都在这两点的连线下方。换句话说,凸函数的局部最小值就是全局最小值。
+
+ +
+#### 判定
+
+**一阶条件:**
+
+对于任意的 $x_1, x_2 \in \mathbb{R}^n$,都有
+
+$$
+f(x_2) \geq f(x_1) + \nabla f(x_1)^T (x_2 - x_1)
+$$
+
+几何意义:任何一点的切线在凸函数曲线的下方。
+
+
+
+**二阶条件:**
+
+对于任意的 $x \in \mathbb{R}^n$,都有
+
+$$
+\nabla^2 f(x) \geq 0
+$$
+
+几何意义:函数曲线向上弯曲。
+
+#### 性质
+
+- 凸函数的非负线性组合仍为凸函数。
+
+- 若 $f(x)$ 是定义在凸集 $\mathbb{R}^n$ 上的凸函数,则其 $\beta$ 水平集 $S_\beta$ 为凸集。
+> 半平面是凸集
+
+- 对于凸函数 $f(x)$,若存在 $x^* \in \mathbb{R}^n$ 满足
+
+$$
+\nabla f(x^*)^T (x - x^*) \geq 0 \quad \forall x \in \mathbb{R}^n
+$$
+
+则 $x^*$ 为 $f(x)$ 的全局最小点。
+
+> 站在山谷底看,哪里都是向上走
+
+- 对于凸目标函数,$\nabla f(x^*) = 0$ 是 $x^*$ 为极小值的充要条件。
+
+- 对于凸目标函数,局部极小点也是全局最小点。
+
+
+
+
+
+
+
+
+
+### 凸优化
+
+
+
+函数是凸函数,可行域是凸集;凹函数求最大值其实是一样的,加一个负号就可以了
+
+
+
+- 任何局部极值解也是全局最优解(目标函数为凸函数)
+
+局部极小点和全局最小点连线的目标函数值相同
+
+- 若目标函数为严格凸函数, 则如果全局最优解存在,必为唯一全局最优解。(反证法)
+ $$
+ f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}^{*}\right]<\lambda f\left(x_{1}^{*}\right)+(1-\lambda) f\left(x_{2}^{*}\right)=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right)
+ $$
+
+最优解的唯一性为数值解法提供了方便。
+
+- 凸规划下的KKT条件为最优解的充要条件
+
+
+
+
+
+
+
+* 线性规划(LP): linprog
+* 混合整数线性规划 (MILP): intlinprog
+* 二次规划(QP): quadprog
+* 二阶锥规划(SOCP): coneprog
+* 半定规划(SDP): Yalmip中调用SDP求解器
+
+* 无约束极值问题: fminunc
+* 有约束极值问题: fmincon
+
+$$
+\text { LPS } \subseteq \text { QPS } \subseteq \text { QCQPS } \subseteq \text { SOCPs } \subseteq \text { SDPs } \subseteq \text { 锥规划 } \mid \text { CPs }
+$$
+
+
+
+线性矩阵不等式LMI
+
+### 方法
+
+- 松弛到更大的区域
+- 分支定解法,拆解成多个凸集进行分布求解
+
+
-
-
-凸优化:函数是凸函数,可行域是凸集;凹函数求最大值其实是一样的,加一个负号就可以了
## 数学模型
+
+
+$$
+\min \quad f(x)
$$
-\min f(x) \\
-\text { s.t. }\left\{
-\begin{array}{c}
- \quad h_{i}(x)=0 \quad i=1,2, \ldots, m \\
-g_{j}(x) \geq 0 \quad j=1,2, \ldots, l \\
-x \in R^{n}
-\end{array}
-\right.
+$$
+\text{s.t.} \quad h_i(x) = 0 \quad i = 1, 2, ..., m
+$$
+
+$$
+\quad g_j(x) \ge 0 \quad j = 1, 2, ..., l
+$$
+
+$$
+x \in R^n
+$$
+
+将等式约束变为不等式约束,可以得到
+
+$$
+\min \quad f(x)\\
+
+\text{s.t.} \quad h_i(x) \ge 0 \quad i = 1, 2, ..., m
+\\
+\quad -h_i(x) \ge 0 \quad i = 1, 2, ..., m
+\\
+\quad g_j(x) \ge 0 \quad j = 1, 2, ..., l
+\\
+x \in R^n
$$
@@ -32,7 +191,80 @@ $$

-## 解析解法:
+
+
+
+
+**原问题**
+
+$$
+\begin{aligned}
+\min_x \ & f_0(x), x \in \mathbb{R}^n \\
+\text{s.t.} \quad & f_i(x) \le 0, \text{其中} i=1,2,3...m \\
+& h_i(x) = 0, \text{其中} i=1,2,3...q
+\end{aligned}
+$$
+
+**等价问题**
+
+$$
+\begin{aligned}
+\min_x \ \max_{\lambda, \nu} \ & L(x, \lambda, \nu)
+= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
+
+\text{s.t.} \quad & \lambda_i \ge 0 \\
+\end{aligned}
+$$
+
+
+等价性的证明
+
+$$
+x \text{在可行域内} \\
+\left\{
+\begin{array}{**lr**}
+ \lambda_i f_i(x) = 0 \quad \text{或} \lambda_i = 0 \quad\text{或} f_i(x) = 0 \\
+\nu_i h_i(x) = 0 \quad\text{或} \nu_i = 0 \quad\text{或} h_i(x) = 0
+\end{array}
+\right.
+$$
+
+* 当$x$在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)$
+* 当$x$不在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty$
+
+因此,$\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)$
+
+
+
+**对偶问题**
+
+$$
+\begin{aligned}
+&\max \limits_{\lambda,v} g(\mathbf{\lambda},\mathbf{v}) = \max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})\\
+&\text{s.t.}
+\left\{
+ \begin{array}{**lr**}
+
+ \nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
+ \lambda \geq0
+ \end{array}
+\right.
+\end{aligned}
+$$
+
+
+
+!!! note "无论原问题是什么问题,对偶问题都是凸问题"
+
+
+
+
+
+
+
+
+
+## 解析解法
### 无约束:
@@ -90,6 +322,7 @@ $$
#### **雅可比矩阵(Jacobian matrix)**
它的重要性在于它体现了一个可微方程与给出点的最优线性逼近,因此,雅可比矩阵类似于多元函数的导数
+
$$
J(\mathbf{f}) = \begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\
@@ -125,6 +358,24 @@ $$
+
+#### 判定
+
+**一阶条件:**
+
+对于任意的 $x_1, x_2 \in \mathbb{R}^n$,都有
+
+$$
+f(x_2) \geq f(x_1) + \nabla f(x_1)^T (x_2 - x_1)
+$$
+
+几何意义:任何一点的切线在凸函数曲线的下方。
+
+
+
+**二阶条件:**
+
+对于任意的 $x \in \mathbb{R}^n$,都有
+
+$$
+\nabla^2 f(x) \geq 0
+$$
+
+几何意义:函数曲线向上弯曲。
+
+#### 性质
+
+- 凸函数的非负线性组合仍为凸函数。
+
+- 若 $f(x)$ 是定义在凸集 $\mathbb{R}^n$ 上的凸函数,则其 $\beta$ 水平集 $S_\beta$ 为凸集。
+> 半平面是凸集
+
+- 对于凸函数 $f(x)$,若存在 $x^* \in \mathbb{R}^n$ 满足
+
+$$
+\nabla f(x^*)^T (x - x^*) \geq 0 \quad \forall x \in \mathbb{R}^n
+$$
+
+则 $x^*$ 为 $f(x)$ 的全局最小点。
+
+> 站在山谷底看,哪里都是向上走
+
+- 对于凸目标函数,$\nabla f(x^*) = 0$ 是 $x^*$ 为极小值的充要条件。
+
+- 对于凸目标函数,局部极小点也是全局最小点。
+
+
+
+
+
+
+
+
+
+### 凸优化
+
+
+
+函数是凸函数,可行域是凸集;凹函数求最大值其实是一样的,加一个负号就可以了
+
+
+
+- 任何局部极值解也是全局最优解(目标函数为凸函数)
+
+局部极小点和全局最小点连线的目标函数值相同
+
+- 若目标函数为严格凸函数, 则如果全局最优解存在,必为唯一全局最优解。(反证法)
+ $$
+ f\left[\lambda x_{1}^{*}+(1-\lambda) x_{2}^{*}\right]<\lambda f\left(x_{1}^{*}\right)+(1-\lambda) f\left(x_{2}^{*}\right)=f\left(x_{1}^{*}\right)=f\left(x_{2}^{*}\right)
+ $$
+
+最优解的唯一性为数值解法提供了方便。
+
+- 凸规划下的KKT条件为最优解的充要条件
+
+
+
+
+
+
+
+* 线性规划(LP): linprog
+* 混合整数线性规划 (MILP): intlinprog
+* 二次规划(QP): quadprog
+* 二阶锥规划(SOCP): coneprog
+* 半定规划(SDP): Yalmip中调用SDP求解器
+
+* 无约束极值问题: fminunc
+* 有约束极值问题: fmincon
+
+$$
+\text { LPS } \subseteq \text { QPS } \subseteq \text { QCQPS } \subseteq \text { SOCPs } \subseteq \text { SDPs } \subseteq \text { 锥规划 } \mid \text { CPs }
+$$
+
+
+
+线性矩阵不等式LMI
+
+### 方法
+
+- 松弛到更大的区域
+- 分支定解法,拆解成多个凸集进行分布求解
+
+
-
-
-凸优化:函数是凸函数,可行域是凸集;凹函数求最大值其实是一样的,加一个负号就可以了
## 数学模型
+
+
+$$
+\min \quad f(x)
$$
-\min f(x) \\
-\text { s.t. }\left\{
-\begin{array}{c}
- \quad h_{i}(x)=0 \quad i=1,2, \ldots, m \\
-g_{j}(x) \geq 0 \quad j=1,2, \ldots, l \\
-x \in R^{n}
-\end{array}
-\right.
+$$
+\text{s.t.} \quad h_i(x) = 0 \quad i = 1, 2, ..., m
+$$
+
+$$
+\quad g_j(x) \ge 0 \quad j = 1, 2, ..., l
+$$
+
+$$
+x \in R^n
+$$
+
+将等式约束变为不等式约束,可以得到
+
+$$
+\min \quad f(x)\\
+
+\text{s.t.} \quad h_i(x) \ge 0 \quad i = 1, 2, ..., m
+\\
+\quad -h_i(x) \ge 0 \quad i = 1, 2, ..., m
+\\
+\quad g_j(x) \ge 0 \quad j = 1, 2, ..., l
+\\
+x \in R^n
$$
@@ -32,7 +191,80 @@ $$

-## 解析解法:
+
+
+
+
+**原问题**
+
+$$
+\begin{aligned}
+\min_x \ & f_0(x), x \in \mathbb{R}^n \\
+\text{s.t.} \quad & f_i(x) \le 0, \text{其中} i=1,2,3...m \\
+& h_i(x) = 0, \text{其中} i=1,2,3...q
+\end{aligned}
+$$
+
+**等价问题**
+
+$$
+\begin{aligned}
+\min_x \ \max_{\lambda, \nu} \ & L(x, \lambda, \nu)
+= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
+
+\text{s.t.} \quad & \lambda_i \ge 0 \\
+\end{aligned}
+$$
+
+
+等价性的证明
+
+$$
+x \text{在可行域内} \\
+\left\{
+\begin{array}{**lr**}
+ \lambda_i f_i(x) = 0 \quad \text{或} \lambda_i = 0 \quad\text{或} f_i(x) = 0 \\
+\nu_i h_i(x) = 0 \quad\text{或} \nu_i = 0 \quad\text{或} h_i(x) = 0
+\end{array}
+\right.
+$$
+
+* 当$x$在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)$
+* 当$x$不在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty$
+
+因此,$\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)$
+
+
+
+**对偶问题**
+
+$$
+\begin{aligned}
+&\max \limits_{\lambda,v} g(\mathbf{\lambda},\mathbf{v}) = \max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})\\
+&\text{s.t.}
+\left\{
+ \begin{array}{**lr**}
+
+ \nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
+ \lambda \geq0
+ \end{array}
+\right.
+\end{aligned}
+$$
+
+
+
+!!! note "无论原问题是什么问题,对偶问题都是凸问题"
+
+
+
+
+
+
+
+
+
+## 解析解法
### 无约束:
@@ -90,6 +322,7 @@ $$
#### **雅可比矩阵(Jacobian matrix)**
它的重要性在于它体现了一个可微方程与给出点的最优线性逼近,因此,雅可比矩阵类似于多元函数的导数
+
$$
J(\mathbf{f}) = \begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\
@@ -125,6 +358,24 @@ $$
 +对于一个二元函数 $f(x, y)$,它的黑塞矩阵是一个 2x2 的矩阵,由函数的二阶偏导数组成。黑塞矩阵的一般形式为:
+
+$$
+H = \begin{bmatrix}
+\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
+\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
+\end{bmatrix}
+$$
+
+由于二阶偏导数具有对称性,即 $\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$,所以黑塞矩阵是一个对称矩阵。因此,我们可以将黑塞矩阵简化为:
+
+$$
+H = \begin{bmatrix}
+\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
+\frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2}
+\end{bmatrix}
+$$
+
无约束极小值问题的最优性条件
@@ -139,7 +390,6 @@ $$
### 有约束
-等式约束
$$
\begin{array}{ll}
\min & f(x) \\
@@ -148,17 +398,6 @@ $$
\end{array}
$$
-等式约束的向量形式
-$$
-\begin{array}{ll}
-\min & f(x) \\
-\text{s.t.} & h(x) = 0 \\
-& x \in \mathbb{R}^n
-\end{array}
-$$
-
-其中,$h(x) = \begin{bmatrix} h_1(x) \\ h_2(x) \\ \vdots \\ h_m(x) \end{bmatrix}$。
-
#### 拉格朗日函数
@@ -185,19 +424,12 @@ $$
+对于一个二元函数 $f(x, y)$,它的黑塞矩阵是一个 2x2 的矩阵,由函数的二阶偏导数组成。黑塞矩阵的一般形式为:
+
+$$
+H = \begin{bmatrix}
+\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
+\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
+\end{bmatrix}
+$$
+
+由于二阶偏导数具有对称性,即 $\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$,所以黑塞矩阵是一个对称矩阵。因此,我们可以将黑塞矩阵简化为:
+
+$$
+H = \begin{bmatrix}
+\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
+\frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2}
+\end{bmatrix}
+$$
+
无约束极小值问题的最优性条件
@@ -139,7 +390,6 @@ $$
### 有约束
-等式约束
$$
\begin{array}{ll}
\min & f(x) \\
@@ -148,17 +398,6 @@ $$
\end{array}
$$
-等式约束的向量形式
-$$
-\begin{array}{ll}
-\min & f(x) \\
-\text{s.t.} & h(x) = 0 \\
-& x \in \mathbb{R}^n
-\end{array}
-$$
-
-其中,$h(x) = \begin{bmatrix} h_1(x) \\ h_2(x) \\ \vdots \\ h_m(x) \end{bmatrix}$。
-
#### 拉格朗日函数
@@ -185,19 +424,12 @@ $$
 -只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为0
-
-
-
-
-
-
-
-
+> 只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为0
不等式约束
+
$$
\begin{array}{ll}
\min & f(x) \\
@@ -208,9 +440,7 @@ $$
-目标函数减小的充分条件
-约束$g(x) = 0$强约束
@@ -293,96 +523,392 @@ $B^T$是$R^n$中一组基,由$m$个$n$维列向量组成,只存在两种情
-#### **Fritz John定理**
+#### **Fritz John定理**——局部极小点必要条件
+
+$$
+\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \mu_i^* \nabla h_i(x^*) + \sum_{i=1}^m \mu_i^{**} \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+$$
+\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m (\mu_i^* - \mu_i^{**}) \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+$$
+\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+其中,$\gamma_i = \mu_i^* - \mu_i^{**}$,并且有:
+
+$$
+\mu_i^* \ge 0 \quad \mu_i^{**} \ge 0 \quad \Longrightarrow \gamma_i = \mu_i^* - \mu_i^{**} \text{ 无符号约束 } \quad i = 1, 2, ..., p
+$$
+
+注意,$\mu_0$、$\mu_j$、$\gamma_i$ 不可同时为 0。
+
+> $\gamma_i$无符号约束,所以前边是加号或是减号都不影响
+
+
+
+
+
+假设 $x^*$ 是局部极小点,存在不全为零的 $\mu_j^* (j=0, 1, 2, ..., m)$ 和 $\gamma_i (i=0, 1, 2, ..., p)$,满足:
+
+$$
+\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0 \quad 拉格朗日条件
+$$
-设$X^*$是非线性规划的局部最优点,函数$f(x)$和$g_j(x)(j=1,2,...,l)$在点$X^*$有连续一阶偏导,则必然存在不全为零的数$\mu_0, \mu_1, \mu_2, ..., \mu_l$,使
+$$
+\mu_j^* g_j(x^*) = 0 \quad j = 1, 2, ..., m \quad 互补松弛条件\\
+\gamma_i h_i(x^*) = 0 \quad i = 1, 2, ..., p \quad 等式互补松弛
+$$
$$
-\begin{align}
-\mu_0 \nabla f(X^*) - \sum_{j=1}^l \mu_j \nabla g_j(X^*) = 0 \quad &Lagrange函数驻点条件\\
-\mu_j g_j(X^*) = 0 \quad (j=1,2,...,l) \quad &互补松弛条件\\
-\mu_0 \ge 0, \mu_j \ge 0 \quad (j=1,2,...,l) \quad &强非负条件
-\end{align}
+\mu_j^* \ge 0 \quad j = 0, 1, ..., m\\
+\sum_{j=0}^l \mu_j^* + \sum_{i=1}^m |\gamma_i^* |\neq 0 \quad 强非负条件
$$
+
+
-只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为0
-
-
-
-
-
-
-
-
+> 只有在相切的时候,可行域的切线和梯度才能在同一方向,相加才可能为0
不等式约束
+
$$
\begin{array}{ll}
\min & f(x) \\
@@ -208,9 +440,7 @@ $$
-目标函数减小的充分条件
-约束$g(x) = 0$强约束
@@ -293,96 +523,392 @@ $B^T$是$R^n$中一组基,由$m$个$n$维列向量组成,只存在两种情
-#### **Fritz John定理**
+#### **Fritz John定理**——局部极小点必要条件
+
+$$
+\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \mu_i^* \nabla h_i(x^*) + \sum_{i=1}^m \mu_i^{**} \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+$$
+\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m (\mu_i^* - \mu_i^{**}) \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+$$
+\Longrightarrow \mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0
+$$
+
+其中,$\gamma_i = \mu_i^* - \mu_i^{**}$,并且有:
+
+$$
+\mu_i^* \ge 0 \quad \mu_i^{**} \ge 0 \quad \Longrightarrow \gamma_i = \mu_i^* - \mu_i^{**} \text{ 无符号约束 } \quad i = 1, 2, ..., p
+$$
+
+注意,$\mu_0$、$\mu_j$、$\gamma_i$ 不可同时为 0。
+
+> $\gamma_i$无符号约束,所以前边是加号或是减号都不影响
+
+
+
+
+
+假设 $x^*$ 是局部极小点,存在不全为零的 $\mu_j^* (j=0, 1, 2, ..., m)$ 和 $\gamma_i (i=0, 1, 2, ..., p)$,满足:
+
+$$
+\mu_0^* \nabla f(x^*) - \sum_{i=1}^m \gamma_i \nabla h_i(x^*) - \sum_{j=1}^l \mu_j^* \nabla g_j(x^*) = 0 \quad 拉格朗日条件
+$$
-设$X^*$是非线性规划的局部最优点,函数$f(x)$和$g_j(x)(j=1,2,...,l)$在点$X^*$有连续一阶偏导,则必然存在不全为零的数$\mu_0, \mu_1, \mu_2, ..., \mu_l$,使
+$$
+\mu_j^* g_j(x^*) = 0 \quad j = 1, 2, ..., m \quad 互补松弛条件\\
+\gamma_i h_i(x^*) = 0 \quad i = 1, 2, ..., p \quad 等式互补松弛
+$$
$$
-\begin{align}
-\mu_0 \nabla f(X^*) - \sum_{j=1}^l \mu_j \nabla g_j(X^*) = 0 \quad &Lagrange函数驻点条件\\
-\mu_j g_j(X^*) = 0 \quad (j=1,2,...,l) \quad &互补松弛条件\\
-\mu_0 \ge 0, \mu_j \ge 0 \quad (j=1,2,...,l) \quad &强非负条件
-\end{align}
+\mu_j^* \ge 0 \quad j = 0, 1, ..., m\\
+\sum_{j=0}^l \mu_j^* + \sum_{i=1}^m |\gamma_i^* |\neq 0 \quad 强非负条件
$$
+
+
 -> 红线上的梯度,在$\lambda_i > 0$的情况下是不可能和目标函数相抵消的,所以只能是$\lambda_i =0$(松弛的约束条件),然后让$x^*$处的约束条件(紧致的约束条件)线性组合为负梯度
+> - 对于紧致的约束条件,$g(x^*) = 0$,但是$\sum_{j=1}^l \mu_j \nabla g_j(X^*)$应该等于负梯度,$\lambda_i \neq 0$
+>
+> - 对于松弛的约束条件,将$x^*$带入方程,一定是小于(大于)0的,最重要的是要让梯度在$\lambda_i$的作用下不对结果起作用;
-> 红线上的梯度,在$\lambda_i > 0$的情况下是不可能和目标函数相抵消的,所以只能是$\lambda_i =0$(松弛的约束条件),然后让$x^*$处的约束条件(紧致的约束条件)线性组合为负梯度
+> - 对于紧致的约束条件,$g(x^*) = 0$,但是$\sum_{j=1}^l \mu_j \nabla g_j(X^*)$应该等于负梯度,$\lambda_i \neq 0$
+>
+> - 对于松弛的约束条件,将$x^*$带入方程,一定是小于(大于)0的,最重要的是要让梯度在$\lambda_i$的作用下不对结果起作用; +
+
+
+#### KKT条件——强对偶的必要条件
+
+正则条件(regular condition)是指起作用约束$\nabla g_{i^*}(x^*)$线性无关。
+
+性质:若极小值$x^*$满足正则条件,则KKT条件成立。证明:$x^*$满足正则条件,Fritz John条件中的$\mu_i>0$。
+
+Kuhn-Tucker定理:若$x^*$是局部极小点,且满足正则条件(约束规格),则Kuhn-Tucker条件成立。
+
+
+
+
+
+
+
+##### **KKT条件的矩阵形式**
+
+$$
+y^* =
+
+\begin{bmatrix}
+y_1^* \\
+y_2^* \\
+\vdots \\
+y_m^*
+\end{bmatrix}
+
+\quad
+h(x)=
+\begin{bmatrix}
+h_1(x) \\
+h_2(x) \\
+\vdots \\
+h_m(x)
+\end{bmatrix}
+
+\quad
+\mu^* =
+\begin{bmatrix}
+\mu_1^* \\
+\mu_2^* \\
+\vdots \\
+\mu_n^*
+\end{bmatrix}
+
+\quad
+g(x) =
+\begin{bmatrix}
+g_1(x) \\
+g_2(x) \\
+\vdots \\
+g_n(x)
+\end{bmatrix}
+$$
+
+$$
+\nabla h(x) =
+\begin{bmatrix}
+\nabla h_1(x) & \nabla h_2(x) & \cdots & \nabla h_m(x)
+\end{bmatrix}
+$$
+
+$$
+\nabla g(x) =
+\begin{bmatrix}
+\nabla g_1(x) & \nabla g_2(x) & \cdots & \nabla g_l(x)
+\end{bmatrix}
+=
+\begin{bmatrix}
+\frac{\partial g_1}{\partial x_1} & \frac{\partial g_2}{\partial x_1} & \cdots & \frac{\partial g_l}{\partial x_1} \\
+\frac{\partial g_1}{\partial x_2} & \frac{\partial g_2}{\partial x_2} & \cdots & \frac{\partial g_l}{\partial x_2} \\
+\vdots & \vdots & \ddots & \vdots \\
+\frac{\partial g_1}{\partial x_n} & \frac{\partial g_2}{\partial x_n} & \cdots & \frac{\partial g_l}{\partial x_n}
+\end{bmatrix}^T
+$$
+
+**Lagrange驻点条件**
+
+$$
+\nabla f(x^*) - \nabla h(x^*)y^* - \nabla g(x^*)\mu^* = 0
+$$
+
+**互补松弛条件**
+
+$$
+\mu^* \odot g(x^*) = 0 \\\Leftrightarrow \mu_j^* g_j(x^*) = 0 \quad j=1,2,...,l
+$$
+
+**非负条件**
+
+$$
+\mu^* \geq 0
+$$
+
+**可行性条件**
+
$$
\begin{aligned}
-\min_x \ & f_0(x), x \in \mathbb{R}^n \\
-\text{s.t.} \quad & f_i(x) \le 0, \text{其中} i=1,2,3...m \\
-& h_i(x) = 0, \text{其中} i=1,2,3...q
+h(x^*) &= 0 \\
+g(x^*) &\geq 0
\end{aligned}
$$
-**等价问题**
+
+
+
+
+#### 例题
+
+$$
+\begin{array}{ll}
+\min & f(x_1, x_2) = (x_1 - 2)^2 + x_2^2 \\
+\text{s.t.} & x_2 \le x_1 + 2 \\
+& x_2 \ge x_1^2 + 1 \\
+& x_1 \ge 0 \quad x_2 \ge 0
+\end{array}
$$
-\begin{aligned}
-\min_x \ \max_{\lambda, \nu} \ & L(x, \lambda, \nu)
-= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
-\text{s.t.} \quad & \lambda_i \ge 0 \\
-\end{aligned}
+**列出向量**
+$$
+f(\mathbf{x}) = (x_1 - 2)^2 + x_2^2
$$
+$$
+\nabla f(\mathbf{x}) = \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right]
+$$
-等价性的证明
$$
-x \text{在可行域内} \\
-\left\{
-\begin{array}{**lr**}
- \lambda_i f_i(x) = 0 \quad \text{或} \lambda_i = 0 \quad\text{或} f_i(x) = 0 \\
-\nu_i h_i(x) = 0 \quad\text{或} \nu_i = 0 \quad\text{或} h_i(x) = 0
+\mathbf{g}(\mathbf{x}) = \left[ \begin{array}{c} x_1 - x_2 + 2 \\ -x_1^2 + x_2 - 1 \\ x_1 \\ x_2 \end{array} \right]
+$$
+
+$$
+\nabla \mathbf{g}(\mathbf{x}) = \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right]
+$$
+
+**列出题目条件**
+$$
+\nabla f(x^*) - \nabla h(x^*) y^* - \nabla g(x^*) \mu^* = 0
+$$
+
+$$
+\Longrightarrow \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right] - \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \mu_1 \\ \mu_2 \\ \mu_3 \\ \mu_4 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
+$$
+
+$$
+\mu^* \otimes g(x^*) = 0 \quad \Longrightarrow \left[ \begin{array}{c} \mu_1 (x_1 - x_2 + 2) \\ \mu_2 (-x_1^2 + x_2 - 1) \\ \mu_3 x_1 \\ \mu_4 x_2 \end{array} \right] = 0
+$$
+
+$$
+g(x^*) \ge 0 \quad \mu^* \ge 0
+$$
+
+**得出方程**
+$$
+\begin{array}{ll}
+2(x_1 - 2) - \mu_1 + 2 \mu_2 x_1 - \mu_3 &= 0 \\
+2x_2 + \mu_1 - \mu_2 - \mu_4 &= 0 \\
+\mu_1 (x_1 - x_2 + 2) &= 0 \\
+\mu_2 (-x_1^2 + x_2 - 1) &= 0 \\
+\mu_3 x_1 &= 0 \\
+\mu_4 x_2 &= 0 \\
+\mu_j &\ge 0 \quad j = 1, 2, 3, 4 \\
+x_2 &\le x_1 + 2 \\
+x_2 &\ge x_1^2 + 1 \\
+x_1, x_2 &\ge 0
\end{array}
-\right.
$$
-* 当$x$在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)$
-* 当$x$不在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty$
+**求解方程**
+观察可得:$\mu_1 = \mu_3 = \mu_4 = 0$(松弛性)
-因此,$\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)$
+所以有:
+$$
+(1 + \mu_2) x_1 - 2 = 0
+$$
+$$
+2x_2 - \mu_2 = 0
+$$
+
+$$
+-x_1^2 + x_2 - 1 = 0
+$$
+
+求解得:
+
+$$
+\mu_2^* = 2.6219 \quad x_1^* = 0.5536 \quad x_2^* = 1.3064
+$$
+
+$$
+f(x^*) = 3.7989
+$$
+
+### 在机器学习中的应用
+
+最大熵
+
+交叉熵
+
+
+
+## 数值解法
+
+包括基于梯度的数值解法,如最速下降法、牛顿法、拟牛顿法等,以及有约束极值问题的数值解法,如可行方向法、制约函数法等。
+
+
+
+
+
+#### KKT条件——强对偶的必要条件
+
+正则条件(regular condition)是指起作用约束$\nabla g_{i^*}(x^*)$线性无关。
+
+性质:若极小值$x^*$满足正则条件,则KKT条件成立。证明:$x^*$满足正则条件,Fritz John条件中的$\mu_i>0$。
+
+Kuhn-Tucker定理:若$x^*$是局部极小点,且满足正则条件(约束规格),则Kuhn-Tucker条件成立。
+
+
+
+
+
+
+
+##### **KKT条件的矩阵形式**
+
+$$
+y^* =
+
+\begin{bmatrix}
+y_1^* \\
+y_2^* \\
+\vdots \\
+y_m^*
+\end{bmatrix}
+
+\quad
+h(x)=
+\begin{bmatrix}
+h_1(x) \\
+h_2(x) \\
+\vdots \\
+h_m(x)
+\end{bmatrix}
+
+\quad
+\mu^* =
+\begin{bmatrix}
+\mu_1^* \\
+\mu_2^* \\
+\vdots \\
+\mu_n^*
+\end{bmatrix}
+
+\quad
+g(x) =
+\begin{bmatrix}
+g_1(x) \\
+g_2(x) \\
+\vdots \\
+g_n(x)
+\end{bmatrix}
+$$
+
+$$
+\nabla h(x) =
+\begin{bmatrix}
+\nabla h_1(x) & \nabla h_2(x) & \cdots & \nabla h_m(x)
+\end{bmatrix}
+$$
+
+$$
+\nabla g(x) =
+\begin{bmatrix}
+\nabla g_1(x) & \nabla g_2(x) & \cdots & \nabla g_l(x)
+\end{bmatrix}
+=
+\begin{bmatrix}
+\frac{\partial g_1}{\partial x_1} & \frac{\partial g_2}{\partial x_1} & \cdots & \frac{\partial g_l}{\partial x_1} \\
+\frac{\partial g_1}{\partial x_2} & \frac{\partial g_2}{\partial x_2} & \cdots & \frac{\partial g_l}{\partial x_2} \\
+\vdots & \vdots & \ddots & \vdots \\
+\frac{\partial g_1}{\partial x_n} & \frac{\partial g_2}{\partial x_n} & \cdots & \frac{\partial g_l}{\partial x_n}
+\end{bmatrix}^T
+$$
+
+**Lagrange驻点条件**
+
+$$
+\nabla f(x^*) - \nabla h(x^*)y^* - \nabla g(x^*)\mu^* = 0
+$$
+
+**互补松弛条件**
+
+$$
+\mu^* \odot g(x^*) = 0 \\\Leftrightarrow \mu_j^* g_j(x^*) = 0 \quad j=1,2,...,l
+$$
+
+**非负条件**
+
+$$
+\mu^* \geq 0
+$$
+
+**可行性条件**
+
$$
\begin{aligned}
-\min_x \ & f_0(x), x \in \mathbb{R}^n \\
-\text{s.t.} \quad & f_i(x) \le 0, \text{其中} i=1,2,3...m \\
-& h_i(x) = 0, \text{其中} i=1,2,3...q
+h(x^*) &= 0 \\
+g(x^*) &\geq 0
\end{aligned}
$$
-**等价问题**
+
+
+
+
+#### 例题
+
+$$
+\begin{array}{ll}
+\min & f(x_1, x_2) = (x_1 - 2)^2 + x_2^2 \\
+\text{s.t.} & x_2 \le x_1 + 2 \\
+& x_2 \ge x_1^2 + 1 \\
+& x_1 \ge 0 \quad x_2 \ge 0
+\end{array}
$$
-\begin{aligned}
-\min_x \ \max_{\lambda, \nu} \ & L(x, \lambda, \nu)
-= f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^q \nu_i h_i(x) \\
-\text{s.t.} \quad & \lambda_i \ge 0 \\
-\end{aligned}
+**列出向量**
+$$
+f(\mathbf{x}) = (x_1 - 2)^2 + x_2^2
$$
+$$
+\nabla f(\mathbf{x}) = \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right]
+$$
-等价性的证明
$$
-x \text{在可行域内} \\
-\left\{
-\begin{array}{**lr**}
- \lambda_i f_i(x) = 0 \quad \text{或} \lambda_i = 0 \quad\text{或} f_i(x) = 0 \\
-\nu_i h_i(x) = 0 \quad\text{或} \nu_i = 0 \quad\text{或} h_i(x) = 0
+\mathbf{g}(\mathbf{x}) = \left[ \begin{array}{c} x_1 - x_2 + 2 \\ -x_1^2 + x_2 - 1 \\ x_1 \\ x_2 \end{array} \right]
+$$
+
+$$
+\nabla \mathbf{g}(\mathbf{x}) = \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right]
+$$
+
+**列出题目条件**
+$$
+\nabla f(x^*) - \nabla h(x^*) y^* - \nabla g(x^*) \mu^* = 0
+$$
+
+$$
+\Longrightarrow \left[ \begin{array}{c} 2(x_1 - 2) \\ 2x_2 \end{array} \right] - \left[ \begin{array}{cccc} 1 & -2x_1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} \mu_1 \\ \mu_2 \\ \mu_3 \\ \mu_4 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
+$$
+
+$$
+\mu^* \otimes g(x^*) = 0 \quad \Longrightarrow \left[ \begin{array}{c} \mu_1 (x_1 - x_2 + 2) \\ \mu_2 (-x_1^2 + x_2 - 1) \\ \mu_3 x_1 \\ \mu_4 x_2 \end{array} \right] = 0
+$$
+
+$$
+g(x^*) \ge 0 \quad \mu^* \ge 0
+$$
+
+**得出方程**
+$$
+\begin{array}{ll}
+2(x_1 - 2) - \mu_1 + 2 \mu_2 x_1 - \mu_3 &= 0 \\
+2x_2 + \mu_1 - \mu_2 - \mu_4 &= 0 \\
+\mu_1 (x_1 - x_2 + 2) &= 0 \\
+\mu_2 (-x_1^2 + x_2 - 1) &= 0 \\
+\mu_3 x_1 &= 0 \\
+\mu_4 x_2 &= 0 \\
+\mu_j &\ge 0 \quad j = 1, 2, 3, 4 \\
+x_2 &\le x_1 + 2 \\
+x_2 &\ge x_1^2 + 1 \\
+x_1, x_2 &\ge 0
\end{array}
-\right.
$$
-* 当$x$在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + 0 + 0 = f_0(x)$
-* 当$x$不在可行域内时,$\max_{\lambda, \nu} L(x, \lambda, \nu) = f_0(x) + \infty + \infty = \infty$
+**求解方程**
+观察可得:$\mu_1 = \mu_3 = \mu_4 = 0$(松弛性)
-因此,$\min \limits_x \max \limits_{\lambda, \nu} L(x, \lambda, \nu) = \min \limits_x f_0(x)$
+所以有:
+$$
+(1 + \mu_2) x_1 - 2 = 0
+$$
+$$
+2x_2 - \mu_2 = 0
+$$
+
+$$
+-x_1^2 + x_2 - 1 = 0
+$$
+
+求解得:
+
+$$
+\mu_2^* = 2.6219 \quad x_1^* = 0.5536 \quad x_2^* = 1.3064
+$$
+
+$$
+f(x^*) = 3.7989
+$$
+
+### 在机器学习中的应用
+
+最大熵
+
+交叉熵
+
+
+
+## 数值解法
+
+包括基于梯度的数值解法,如最速下降法、牛顿法、拟牛顿法等,以及有约束极值问题的数值解法,如可行方向法、制约函数法等。
+
+ +
+### 基于梯度方法
+
+#### 最速下降法——迭代初期
+
+
+
+极小值附近的等值面是椭球面
+
+$X^T \cdot \mathbf{H} \cdot X = c$
+
+- 如果$\mathbf{H}$是对角矩阵,则显然是椭圆
+- 如果不是的话,相似对角化以后$X^TM^T \ \Lambda\mathbf{}\ M X = c$
+
+
+
+
+
+
+
+
+
+#### 牛顿法——极值点附近
+
+* 设计思想:近似为二次问题。
-**对偶问题**
$$
\begin{aligned}
-&\max \limits_{\lambda,v} g(\mathbf{\lambda},\mathbf{v}) = \max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})\\
-&\text{s.t.}
-\left\{
- \begin{array}{**lr**}
-
- \nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
- \lambda \geq0
- \end{array}
-\right.
+&f(x) \approx f\left(x^{(k)}\right)+\nabla f\left(x^{(k)}\right)^{T}\left(x-x^{(k)}\right)+\frac{1}{2}\left(x-x^{(k)}\right)^{T} \nabla^{2} f\left(x^{(k)}\right)\left(x-x^{(k)}\right) \\
+&\text { 驻点条件 } \Longrightarrow \nabla f(x) \approx \nabla f\left(x^{(k)}\right)+\nabla^{2} f\left(x^{(k)}\right)\left(x-x^{(k)}\right) \approx 0 \\
+&\text { 迭代公式 } \Longrightarrow x^{(k+1)} \approx x^{(k)}-\left[\nabla^{2} f\left(x^{(k)}\right)\right]^{-1} \nabla f\left(x^{(k)}\right) \\
+&\text { 迭代方向 } \Longrightarrow p^{(k)}=-\left[\nabla^{2} f\left(x^{(k)}\right)\right]^{-1} \nabla f\left(x^{(k)}\right) \quad \text { 牛顿方向 }
\end{aligned}
$$
-
-!!! note "无论原问题是什么问题,对偶问题都是凸问题"
+优点:极值点附近收敛速率快。
+缺点:计算量大,需要求二阶导数和Hessian矩阵逆。
+远离极值点时,不一定是下降方向,需采用进一步修正。
+应用场合:二次目标函数或极值点附近。
+* 设$A$为对称矩阵,二次函数 $f(x)=\frac{1}{2} x^T A x+b^T x+c$
+* 驻点方程: $\nabla f(x)=Ax+b=0$
+ + 有解: $\text{rank} A=\text{rank}[A \quad b]$
+ + 无解: $\text{rank} A \neq \text{rank}[A \quad b]$
+* Hessian矩阵: $\nabla^2 f(x)=A$
-## 数值解法
+例: 抛物面
+
+* (1) $A>0$ 椭球面: $x^*=A^{-1} b$ 唯一极小点
+* (2) $A \geq 0 \quad \& \quad \text{rank} A
+
+### 基于梯度方法
+
+#### 最速下降法——迭代初期
+
+
+
+极小值附近的等值面是椭球面
+
+$X^T \cdot \mathbf{H} \cdot X = c$
+
+- 如果$\mathbf{H}$是对角矩阵,则显然是椭圆
+- 如果不是的话,相似对角化以后$X^TM^T \ \Lambda\mathbf{}\ M X = c$
+
+
+
+
+
+
+
+
+
+#### 牛顿法——极值点附近
+
+* 设计思想:近似为二次问题。
-**对偶问题**
$$
\begin{aligned}
-&\max \limits_{\lambda,v} g(\mathbf{\lambda},\mathbf{v}) = \max \limits_{\lambda,v} \ \min \limits_x \ L(x,\mathbf{\lambda},\mathbf{v})\\
-&\text{s.t.}
-\left\{
- \begin{array}{**lr**}
-
- \nabla_x \ L(x,\mathbf{\lambda},\mathbf{v}) = 0\\
- \lambda \geq0
- \end{array}
-\right.
+&f(x) \approx f\left(x^{(k)}\right)+\nabla f\left(x^{(k)}\right)^{T}\left(x-x^{(k)}\right)+\frac{1}{2}\left(x-x^{(k)}\right)^{T} \nabla^{2} f\left(x^{(k)}\right)\left(x-x^{(k)}\right) \\
+&\text { 驻点条件 } \Longrightarrow \nabla f(x) \approx \nabla f\left(x^{(k)}\right)+\nabla^{2} f\left(x^{(k)}\right)\left(x-x^{(k)}\right) \approx 0 \\
+&\text { 迭代公式 } \Longrightarrow x^{(k+1)} \approx x^{(k)}-\left[\nabla^{2} f\left(x^{(k)}\right)\right]^{-1} \nabla f\left(x^{(k)}\right) \\
+&\text { 迭代方向 } \Longrightarrow p^{(k)}=-\left[\nabla^{2} f\left(x^{(k)}\right)\right]^{-1} \nabla f\left(x^{(k)}\right) \quad \text { 牛顿方向 }
\end{aligned}
$$
-
-!!! note "无论原问题是什么问题,对偶问题都是凸问题"
+优点:极值点附近收敛速率快。
+缺点:计算量大,需要求二阶导数和Hessian矩阵逆。
+远离极值点时,不一定是下降方向,需采用进一步修正。
+应用场合:二次目标函数或极值点附近。
+* 设$A$为对称矩阵,二次函数 $f(x)=\frac{1}{2} x^T A x+b^T x+c$
+* 驻点方程: $\nabla f(x)=Ax+b=0$
+ + 有解: $\text{rank} A=\text{rank}[A \quad b]$
+ + 无解: $\text{rank} A \neq \text{rank}[A \quad b]$
+* Hessian矩阵: $\nabla^2 f(x)=A$
-## 数值解法
+例: 抛物面
+
+* (1) $A>0$ 椭球面: $x^*=A^{-1} b$ 唯一极小点
+* (2) $A \geq 0 \quad \& \quad \text{rank} A